国考1号14·第14套高中2023届高考适应性考试文数试题 答案

国考1号14·第14套高中2023届高考适应性考试文数试题 答案，目前我们已经整理了国考1号14·第14套高中2023届高考适应性考试文数试题 答案的各科答案和试卷，更多国考1号答案请关注本网站。

,如图，P是椭圆子+片=1在第一象限上一点，A,B,C是椭圆与坐标轴的交点，0为坐标原点，过A作AN平行于直线BP交y轴于点N,直线CP交x轴于点M,直线BP交x轴于点E,现有下列三个式子：①10E1·1ON;②1OE1·10M:③OM其中为定值的所有序号是A.①③B.②③C.①②D.①②③【答案】D【解析】设P(xy),所以有5+背=1，又B(0,-5,C(0,5),A(-2,0,所以如·即=为-5+好-3-一333Xolyk-ykxy-n+yw=装t10E11oN1-2,0eoM1=g引·g1-48-后ION=2×3√42,故①②③均为定值.

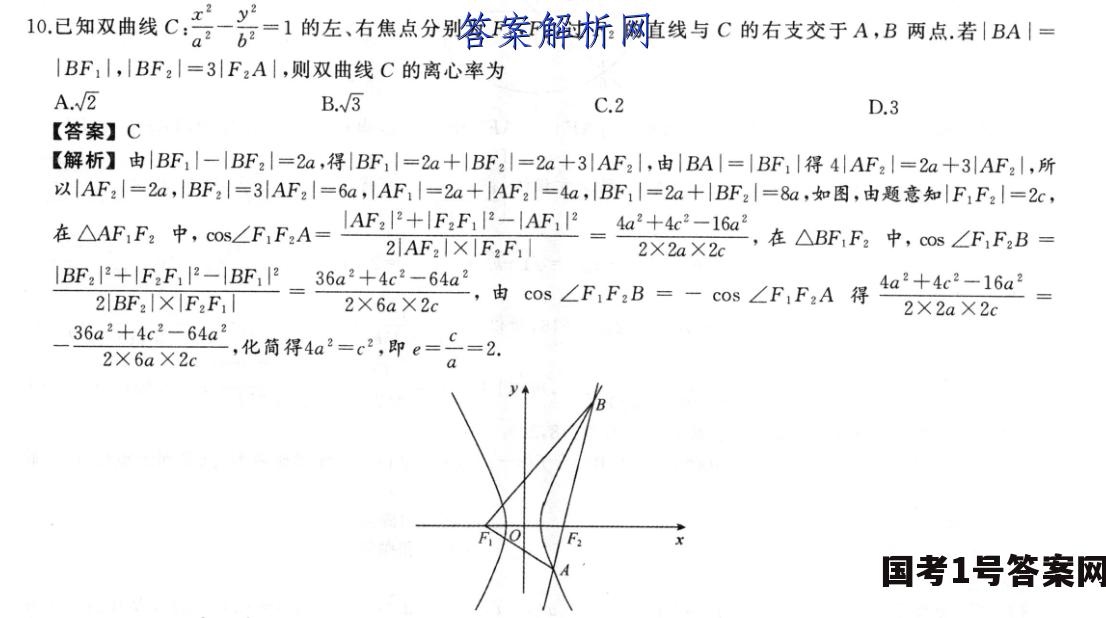
1o,已知双曲线C若方=1的左、右焦点分别为F1,F2,过F:的直线与C的右支交于A,B两点.若1BA1=IBF1I,BF2|=3|F2A|,则双曲线C的离心率为A.√2B.√3C.2D.3【答案】C【解析】由BF1|-|BF2|=2a,得BF,|=2a+|BF2|=2a+3|AF2|,由|BA|=|BF1|得4AF2|=2a+3|AF2|,所以|AF2|=2a,BF2|=3|AF2|=6a,lAF1=2a+|AF2|=4a,lBF1|=2a+|BF2|=8a,如图，由题意知|F:F2|=2c,在△AF,F,中，cs∠F,FA=AFTAEEXERAF=如t6a,在△BF,F,中，os∠F,FB2AF2I×|F2F:2X2a X2c1BF2|2+|F2F|2-|BF1|236a2+4c2-64a22BF2XF2F2X6a X2c由cos∠F,F,B=-cos∠F,F2A得4at4c2-16a22×2aX2c36a2+4c2-64a2X6a X2c,化简得4a2=c2,即e=￡=2.0