国考1号14·第14套高中2023届高考适应性考试文综试题 答案

国考1号14·第14套高中2023届高考适应性考试文综试题 答案，目前我们已经整理了国考1号14·第14套高中2023届高考适应性考试文综试题 答案的各科答案和试卷，更多国考1号答案请关注本网站。

5.已知A(1,0,0),B(0,1,0),C(0,0,1),D(1,1,2),则点D到平面ABC的距离为A.√3B.√2√56C.2D.3【答案】A【解析】依题意，AB=(-1,1,0),AC=(-1,0,1),AD=(0,1,2),设平面ABC的一个法向量为n=(x,y,z),/n·AB=-x+y=0,则n·AC=-x十z=0,x=1,得n=(1,1,1),则点D到平面ABC的距离为d=n·AD-1×1+1×2n12+12+1√3，所以，点D到平面ABC的距离为√3.

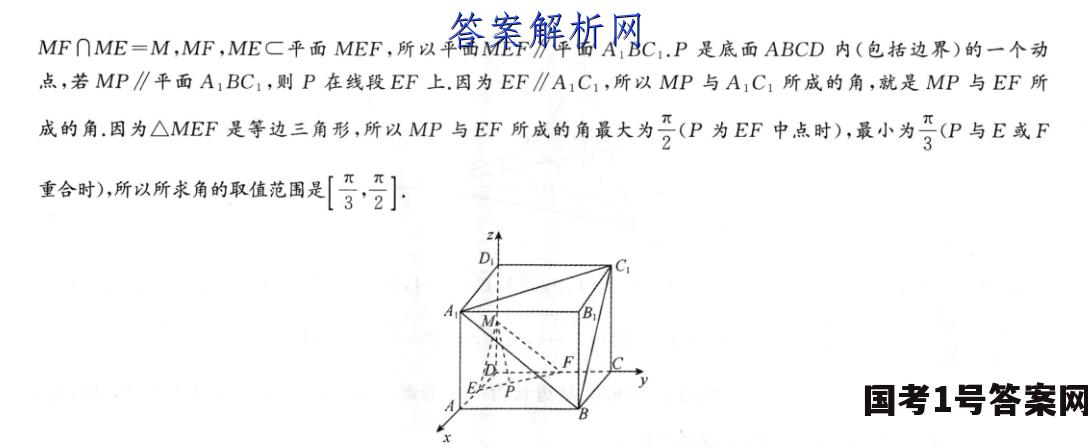
4.在正方体ABCD-A1B,C,D1中，M是棱DD1的中点，P是底面ABCD内（包括边界）的一个动点.若MP∥平面A,BC1,则异面直线MP与A,C1所成角的取值范围是A(0,]B[】c[]【答案】C【解析】如图，以DA,DC,DD1所在直线分别为x,y,之轴建立空间直角坐标系，设AB=2,则A(2,0,0),B(2,2,0),C(0,2,0),A1(2,0,2),C1(0,2,2),D1(0,0,2),M(0,0,1),取AD的中点E,DC的中点F,连接ME,EF,MF,则E(1,0,0),F(0,1,0),ME=(1,0,-1),C1B=(2,0,-2)=2ME,所以C1B∥ME,同理EF∥A,C1,又ME丈平面A1BC1,BC1C平面A1BC1,所以ME∥平面A1BC1,同理MF∥平面A1BC1,而MF∩ME=M,MF,MEC平面MEF,所以平面MEF∥平面A1BC1.P是底面ABCD内（包括边界）的一个动,点，若MP∥平面A1BC1,则P在线段EF上.因为EF∥A1C1,所以MP与A1C1所成的角，就是MP与EF所成的角.因为△MEF是等边三角形，所以MP与EF所成的角最大为2(P为EF中点时)，最小为(P与E或F重合时)，所以所求角的取值范国是[行·]