国考1号14·第14套高中2023届高考适应性考试理综试题 答案

国考1号14·第14套高中2023届高考适应性考试理综试题 答案，目前我们已经整理了国考1号14·第14套高中2023届高考适应性考试理综试题 答案的各科答案和试卷，更多国考1号答案请关注本网站。

21.(12分)已知圆O1:x2+y2=3,圆O2:x2十y2=4,端点为原点的射线l交圆O1于M,交圆O2于N,过M作平行（或重合)于x轴的直线l1,过N作平行（或重合）于y轴的直线L2,l1与L2交于点E.记E的轨迹为曲线C.(1)求C的方程；(2)若A,B是曲线C与x轴的交点(xA

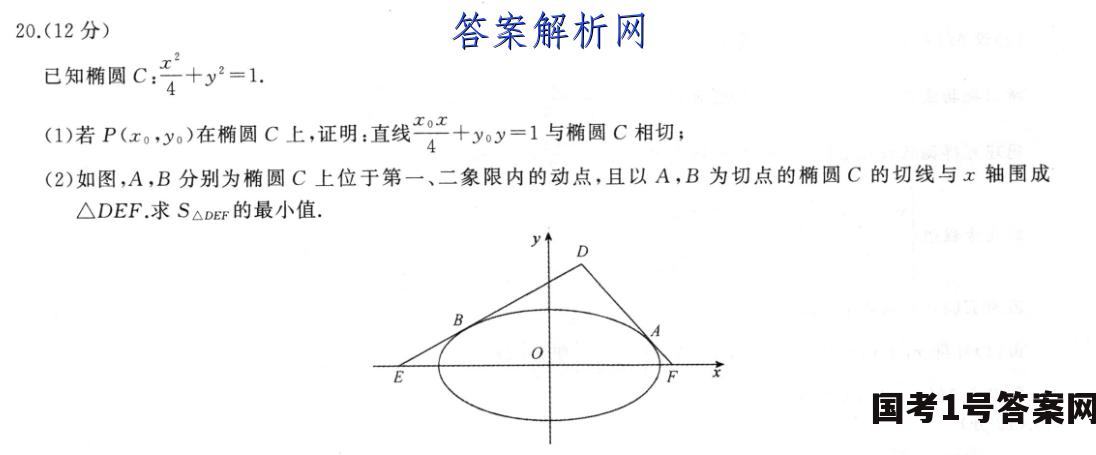
20.(12分)22已知椭圆C:4十y=1.1)若P(x)在椭圆C上，证明：直线+yy=1与椭圆C相切：(2)如图，A,B分别为椭圆C上位于第一、二象限内的动点，且以A,B为切点的椭圆C的切线与x轴围成△DEF.求S△DEF的最小值D夕0Ex(1)证明：由{子十1消去y可得+41-受)广-48，格合+=1，整理得-2+4x2+4y2=4,4y8=0,显然△=4红+16好-16=0，即直线+y0y=1与精圆C有度一公共点，所以直线父+yy=1与精圈C相切.(2)解：依题意，设直线AB:y=kx十m(0 0,即4k2+1>m2,4(m2-1)x1x2=1+4k2(x1-x2)2=(x1十x2)2-4x1x=64k2m216(m2-1)16(4k2-m2+1)1+4k2)31+4k2(1+4k2)3则(SA0er)2=42x:)=4(42+1-m3)41-m)44m2(x1x2)2=m2(1-m2)2m2(1-m2)2m2(1-m2)≥=16,m2+1-m22所以S△Dr≥4，当k=0,m=乞时取等号，所以S△DEF的最小值为4.